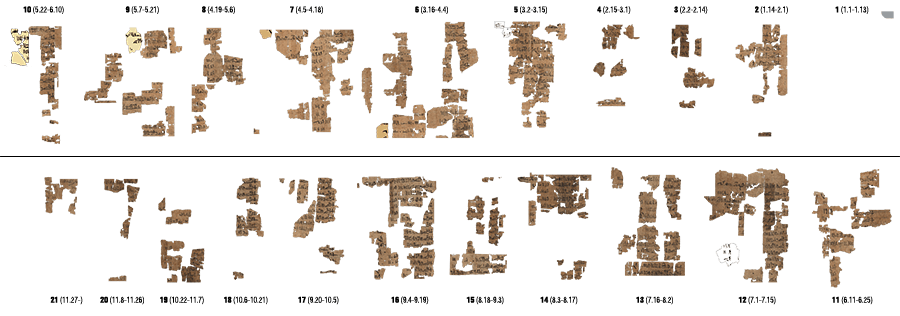The template for the king list
Examining the king list, it quickly becomes obvious that it must be a copy of an older manuscript as first proposed by Helck in 1956, suggesting a literatim copy of a smaller papyrus, since transferring a text from a half-size papyrus to a full-size papyrus would require adjustment of the headings and ditto marks. A Vorlage is basically an earlier version of a text (from the German for prototype or template). The objective of the copyist was clearly not to create a new document, but rather to produce an exact copy of an older original, preserving the text as written. Whether or not the intention was to add newer kings not present in the original to the end of the list of kings is irrelevant.
It is immediately noticable that the reigns are recorded in different ways, and some kings even have their age recorded, while most only record years reigned. The more ancient parts also contain more corrupted names. It all point to that at least five sources were used to create the first king list. The details contained in these ancient records are unknown to us, but can be divided into five sections:
- Source A — Dynasties 1–2, recording years, months, days and the age of the king.
- Source B — Dynasties 3–6, recording only years.
- Source C — Dynasties 7–10, recording years, months and days.
- Source D — Dynasty 11, only recording years
- Source E — Dynasty 12, recording years, months and days.
The resulting king list was merged from these sources (A to E), and compiled into a single document, that would serve as a prototype, or vorlage (from the German for ‘prototype or template of a prior version of a text’). There are several clues found in the text and layout of the Turin King List that point to it being a copy of another papyrus.
The transmission, or lineage of the descendants to the original manuscript, suggest the following:
- It is unknown when the ‘first’ list of kings was created, but probably sometime during the New Kingdom. We refer to this as Vorlage A, from which all subsequent documents are derived.
- From this original, a direct copy was made, designated Vorlage B. This copy suffered damage, and part of the text was lost, or became unreadable.
-
This prompted another copy, Vorlage C, with the damaged parts marked with Lacuna notations
–
wsf – meaning unreadable or lost. - A diligent scribe noticed that there were chronological gaps, and his copy, Vorlage D, emended the lacuna notations by adding 6 years to the gaps.
- Vorlage E was a direct copy of Vorlage D, but on a half-size papyrus. The kingship formula was used for the first king of each dynasty and at the top of each column, while repetition marks were used in the entries following below.
- The Turin King List is a literatim copy of Vorlage E, but on a full-size papyrus.
It is unclear whether any of the vorlages were updated to include any of the New Kingdom pharaohs, depending on whether it was a copy made to preserve, or update, the information held on the older papyrus. With both the start and end of the papyrus lost in lacuna, it is impossible to tell. However, there isn't enough space in the remaining fragments at the end to hold more names, although it is possible that there was a lost twelfth column.
The king list was certainly not a formal document, as the scribe copied it unto a previously used, and damaged papyrus roll. This suggest that it was not intended to be archived, but perhaps only served as an excercise or intermediary for another document.
The following figure sums up the transmission:
After Ryholt, Political Situation, Table 7, p. 32
The nature of a full-size papyrus means that the lines are naturally longer than in a half-size, as there are more vertical surface to write the columns on. Copying a text from a small to a large document requires the adjustment of any ditto-markings to conform to the new and larger papyrus. That this was not done in the Turin King List is a clear indication that the scribe copied Vorlage E sign-by-sign, making an exact copy, without realigning the content. It also explains why there are ditto-marks in the top rows in columns 4 and 9, and also why the kingship formula occur at irregular intervals within the columns.
Reconstruction of the papyrus that the king list was copied from, i.e. Vorlage E, the half-size papyrus with the exact same writing, was first attempted by Malek in 1982. A couple problems with his reconstruction was rejected by Ryholt, who proposed an improved arrangement.
It is well known that writing the same text over and over is tedious and often unnecessary. The scribes of Egypt had long since learned to use ditto marks for repeating words or sentences. A hieratic ditto mark simply consist of either a horizontal line or a dot, and were used in the king list to replace texts. The name of each king is followed by the text “he acted in kingship” which was only written out at the top of a column. Ditto marks were used for the ligatures for months, and days, but not for the years ligature. Numbers were always written out in full.
The full formula for an entry reads:
Dual King Name. He acted in kingship x years, y months and z days.
Ditto marks are not used for the kingship formula in the rows below the top row, but instead left blank and tabulated so that the length of reign in the next row appear at the same horizontal position as the year ligature above. Using ditto marks, the row looks like this:
Dual King Name. He acted in kingship x years, y months and z days.
Though the kingship formula was left blank and not indicated by ditto marks, the structure of the rows certainly suggest its presence. Occasionally the reign figures appear directly following the king's cartouche, without any blank gap, presumably to conserve horizontal space. The fully written out kingship formula is repeated throughout the king list, but not heading the columns as expected, but at seemingly random places in the columns.
The formula appearing at regular intervals every 13 to 16 rows is a clear indication that the original papyrus was a half-sized roll. Moreover, the distance between the rows with the formula increase slightly in the later columns, indicating that the original columns held more rows as the writing progressed, and suggesting that the writing decreased in size as the number of rows in each column increased.
Normally a scribe writes the full text at the top of the page, then use ditto marks on the subsequent rows for repeating text, and then only have to fill in the differing parts. This obviously have the advantage of being faster to write, being more aesthetically pleasing to the eye, and easier to add or update records. The scribe copied the original manuscript without consideration of the text, and did not adjust the ditto marks, which is obvious as they appear in the top row of columns 4, 8, and 9. If it was an adjusted manuscript, the top rows would contain the full text, and certainly not ditto marks.
Generally two types of ditto marks are found in papyri: horizontal lines, and small dots. Both types are found on this papyrus, while the tax-register marks are longer, fitting well with an adminstrative papyrus.
There are a total of 301 rows accounted for in the king list. Note that 3.14 should be discounted (see below), bringing the number to an even 300.
Let us take a look at where the kingship formulas appear:
Complete formula:
| 3.2 | |
| 4.19 | |
| 6.20 | king after heading |
| 7.1 | |
| 8.3 | |
| 9.4 | |
| 11.27 |
Now for the partial formula, i.e. where the initial
Partial formula:
| 2.4 | unlikely |
| 3.11 | king after heading |
| 4.5 | |
| 5.7 | probable |
| 5.22 | unlikely |
| 7.5 | king after heading |
| 7.16 | unlikely |
| 9.20 | unlikely |
Formula expected, but lost/missing:
| 1.1 | Lacuna |
| 1.14 | |
| 2.2 | |
| 2.15 | unreadable |
| 3.16 | |
| 8.18 | Lacuna |
| 10.6 | |
| 10.22 | Lacuna |
| 11.8 |
Tablulating the three kingship formulas, presents the following table:
| 7.1 | Full kingship formula | 7.1 | Partial kingship formula |
| 7.1 | Lost kingship formula | 7.1 | Partial formula for founder of dynasty |
| 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 11.1 | 10.1 | 9.1 | 8.1 | 7.1 | 6.1 | 5.1 | 4.1 | 3.1 | 2.1 | 1.1 |
| 11.2 | 10.2 | 9.2 | 8.2 | 7.2 | 6.2 | 5.2 | 4.2 | 3.2 | 2.2 | 1.2 |
| 11.3 | 10.3 | 9.3 | 8.3 | 7.3 | 6.3 | 5.3 | 4.3 | 3.3 | 2.3 | 1.3 |
| 11.4 | 10.4 | 9.4 | 8.4 | 7.4 | 6.4 | 5.4 | 4.4 | 3.4 | 2.4 | 1.4 |
| 11.5 | 10.5 | 9.5 | 8.5 | 7.5 | 6.5 | 5.5 | 4.5 | 3.5 | 2.5 | 1.5 |
| 11.6 | 10.6 | 9.6 | 8.6 | 7.6 | 6.6 | 5.6 | 4.6 | 3.6 | 2.6 | 1.6 |
| 11.7 | 10.7 | 9.7 | 8.7 | 7.7 | 6.7 | 5.7 | 4.7 | 3.7 | 2.7 | 1.7 |
| 11.8 | 10.8 | 9.8 | 8.8 | 7.8 | 6.8 | 5.8 | 4.8 | 3.8 | 2.8 | 1.8 |
| 11.9 | 10.9 | 9.9 | 8.9 | 7.9 | 6.9 | 5.9 | 4.9 | 3.9 | 2.9 | 1.9 |
| 11.10 | 10.10 | 9.10 | 8.10 | 7.10 | 6.10 | 5.10 | 4.10 | 3.10 | 2.10 | 1.10 |
| 11.11 | 10.11 | 9.11 | 8.11 | 7.11 | 6.11 | 5.11 | 4.11 | 3.11 | 2.11 | 1.11 |
| 11.12 | 10.12 | 9.12 | 8.12 | 7.12 | 6.12 | 5.12 | 4.12 | 3.12 | 2.12 | 1.12 |
| 11.13 | 10.13 | 9.13 | 8.13 | 7.13 | 6.13 | 5.13 | 4.13 | 3.13 | 2.13 | 1.13 |
| 11.14 | 10.14 | 9.14 | 8.14 | 7.14 | 6.14 | 5.14 | 4.14 | 3.15 | 2.14 | 1.14 |
| 11.15 | 10.15 | 9.15 | 8.15 | 7.15 | 6.15 | 5.15 | 4.15 | 3.16 | 2.15 | 1.15 |
| 11.16 | 10.16 | 9.16 | 8.16 | 7.16 | 6.16 | 5.16 | 4.16 | 3.17 | 2.16 | 1.16 |
| 11.17 | 10.17 | 9.17 | 8.17 | 7.17 | 6.17 | 5.17 | 4.17 | 3.18 | 2.17 | 1.17 |
| 11.18 | 10.18 | 9.18 | 8.18 | 7.18 | 6.18 | 5.18 | 4.18 | 3.19 | 2.18 | 1.18 |
| 11.19 | 10.19 | 9.19 | 8.19 | 7.19 | 6.19 | 5.19 | 4.19 | 3.20 | 2.19 | 1.19 |
| 11.20 | 10.20 | 9.20 | 8.20 | 7.20 | 6.20 | 5.20 | 4.20 | 3.21 | 2.20 | 1.20 |
| 11.21 | 10.21 | 9.21 | 8.21 | 7.21 | 6.21 | 5.21 | 4.21 | 3.22 | 2.21 | 1.21 |
| 11.22 | 10.22 | 9.22 | 8.22 | 7.22 | 6.22 | 5.22 | 4.22 | 3.23 | 2.22 | 1.22 |
| 11.23 | 10.23 | 9.23 | 8.23 | 7.23 | 6.23 | 5.23 | 4.23 | 3.24 | 2.23 | 1.23 |
| 11.24 | 10.24 | 9.24 | 8.24 | 7.24 | 6.24 | 5.24 | 4.24 | 3.25 | 2.24 | 1.24 |
| 11.25 | 10.25 | 9.25 | 8.25 | 7.25 | 6.25 | 5.25 | 4.25 | 2.25 | 1.25 | |
| 11.26 | 10.26 | 9.26 | 8.26 | 7.26 | 5.26 | 4.26 | 2.26 | |||
| 11.27 | 10.27 | 9.27 | 8.27 | 7.27 | ||||||
| 11.28 | 10.28 | 9.28 | 8.28 | 7.28 | ||||||
| 11.29 | 10.29 | 9.29 | 8.29 | |||||||
| 11.30 | 10.30 | 9.30 | ||||||||
| 11.31 | 10.31 | |||||||||
| 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
The pattern of the kingship formulas is obvious (especially between 4.5—9.20), appearing every 14-15 rows, suggesting the column height of Vorlage E. The Turin King List is a direct copy of Vorlage E, but on a full-size papyrus. This means that the number of rows in Vorlage E should be roughly the half of that of the king list which is a full-size papyrus.
From 4.5 to 8.3 there are 8 kingship formulas appearing every 14-15 rows. This means that that the preceding columns in Vorlage E should have a maximum of 14 rows per column. Assuming that the top rows of each column in Vorlage E contained the full kingship formula, we can extrapolate the number of rows between the known formulas.
The number of rows from 1.1 to 4.4, i.e. before the kingship formula in 4.5, is 79 (Column 1: 25, Column 2: 26, Column 3: 24, and Column 4: 4). Six columns each with 14 rows yield a total of 84 rows, which is five too many. That means that for the numbers to add up, five columns could only have held 13 rows, and one with 14. Note that 3.14 is delineated with a sort of bracket that enclose the end of the row to differentiate that it belongs to the entry of previous column. To the right of 3.14 in Vorlage E would have been a long 2.26, which was copied by the scribe as it appeared. Starting a new column, the scribe miscalculated the length of Vorlage E row 2.26 by not leaving enough horizontal space, as it would intrude on 3.14.
When 3.14 was reached, a sort of bracket was written around the end of the intruding row (as can also be seen in 5.16 and 8.3) and the king list then continued on the next row. Unlike 5.16 and 8.3, the scribe did not add a king on 3.14, perhaps because he had not yet realized that space would be a problem later on in the king list.
Putting it all together:
| Column | Rows/Columns | Rows |
|---|---|---|
| 1 | 1.1—1.13 | 13 |
| 2 | 1.14—2.1 | 13 |
| 3 | 2.2—2.14 | 13 |
| 4 | 2.15—3.1 | 13 |
| 5 | 3.2—3.15 | 13 |
| 6 | 3.16—4.4 | 14 |
| 7 | 4.5—4.18 | 14 |
| 8 | 4.19—5.6 | 14 |
| 9 | 5.7—5.21 | 15 |
| 10 | 5.22—6.10 | 15 |
| 11 | 6.11—6.25 | 15 |
| 12 | 7.1—7.15 | 15 |
| 13 | 7.16—8.2 | 15 |
| 14 | 8.3—8.17 | 15 |
| 15 | 8.18—9.3 | 15 |
| 16 | 9.4—9.19 | 16 |
| 17 | 9.20—10.5 | 16 |
| 18 | 10.6—10.21 | 16 |
| 19 | 10.22—11.7 | 17 |
| 20 | 11.8—11.26 | 19 |
| 21 | 11.27—lost | 5+x |
Adding the headings, summations and ditto marked rows to the layout, the complete king list looks like this:
| 7.1 | Kingship formula | 7.1 | Lost kingship formula | 7.1 | Partial kingship formula |
| 7.1 | Heading | 7.1 | Lost Heading | 7.1 | Summation |
| 7.1 | Ditto mark | 7.1 | Partial formula for the founder of dynasty | ||
| 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 11.1 | 10.1 | 9.1 | 8.1 | 7.1 | 6.1 | 5.1 | 4.1 | 3.1 | 2.1 | 1.1 |
| 11.2 | 10.2 | 9.2 | 8.2 | 7.2 | 6.2 | 5.2 | 4.2 | 3.2 | 2.2 | 1.2 |
| 11.3 | 10.3 | 9.3 | 8.3 | 7.3 | 6.3 | 5.3 | 4.3 | 3.3 | 2.3 | 1.3 |
| 11.4 | 10.4 | 9.4 | 8.4 | 7.4 | 6.4 | 5.4 | 4.4 | 3.4 | 2.4 | 1.4 |
| 11.5 | 10.5 | 9.5 | 8.5 | 7.5 | 6.5 | 5.5 | 4.5 | 3.5 | 2.5 | 1.5 |
| 11.6 | 10.6 | 9.6 | 8.6 | 7.6 | 6.6 | 5.6 | 4.6 | 3.6 | 2.6 | 1.6 |
| 11.7 | 10.7 | 9.7 | 8.7 | 7.7 | 6.7 | 5.7 | 4.7 | 3.7 | 2.7 | 1.7 |
| 11.8 | 10.8 | 9.8 | 8.8 | 7.8 | 6.8 | 5.8 | 4.8 | 3.8 | 2.8 | 1.8 |
| 11.9 | 10.9 | 9.9 | 8.9 | 7.9 | 6.9 | 5.9 | 4.9 | 3.9 | 2.9 | 1.9 |
| 11.10 | 10.10 | 9.10 | 8.10 | 7.10 | 6.10 | 5.10 | 4.10 | 3.10 | 2.10 | 1.10 |
| 11.11 | 10.11 | 9.11 | 8.11 | 7.11 | 6.11 | 5.11 | 4.11 | 3.11 | 2.11 | 1.11 |
| 11.12 | 10.12 | 9.12 | 8.12 | 7.12 | 6.12 | 5.12 | 4.12 | 3.12 | 2.12 | 1.12 |
| 11.13 | 10.13 | 9.13 | 8.13 | 7.13 | 6.13 | 5.13 | 4.13 | 3.13 | 2.13 | 1.13 |
| 11.14 | 10.14 | 9.14 | 8.14 | 7.14 | 6.14 | 5.14 | 4.14 | 3.15 | 2.14 | 1.14 |
| 11.15 | 10.15 | 9.15 | 8.15 | 7.15 | 6.15 | 5.15 | 4.15 | 3.16 | 2.15 | 1.15 |
| 11.16 | 10.16 | 9.16 | 8.16 | 7.16 | 6.16 | 5.16 | 4.16 | 3.17 | 2.16 | 1.16 |
| 11.17 | 10.17 | 9.17 | 8.17 | 7.17 | 6.17 | 5.17 | 4.17 | 3.18 | 2.17 | 1.17 |
| 11.18 | 10.18 | 9.18 | 8.18 | 7.18 | 6.18 | 5.18 | 4.18 | 3.19 | 2.18 | 1.18 |
| 11.19 | 10.19 | 9.19 | 8.19 | 7.19 | 6.19 | 5.19 | 4.19 | 3.20 | 2.19 | 1.19 |
| 11.20 | 10.20 | 9.20 | 8.20 | 7.20 | 6.20 | 5.20 | 4.20 | 3.21 | 2.20 | 1.20 |
| 11.21 | 10.21 | 9.21 | 8.21 | 7.21 | 6.21 | 5.21 | 4.21 | 3.22 | 2.21 | 1.21 |
| 11.22 | 10.22 | 9.22 | 8.22 | 7.22 | 6.22 | 5.22 | 4.22 | 3.23 | 2.22 | 1.22 |
| 11.23 | 10.23 | 9.23 | 8.23 | 7.23 | 6.23 | 5.23 | 4.23 | 3.24 | 2.23 | 1.23 |
| 11.24 | 10.24 | 9.24 | 8.24 | 7.24 | 6.24 | 5.24 | 4.24 | 3.25 | 2.24 | 1.24 |
| 11.25 | 10.25 | 9.25 | 8.25 | 7.25 | 6.25 | 5.25 | 4.25 | 2.25 | 1.25 | |
| 11.26 | 10.26 | 9.26 | 8.26 | 7.26 | 5.26 | 4.26 | 2.26 | |||
| 11.27 | 10.27 | 9.27 | 8.27 | 7.27 | ||||||
| 11.28 | 10.28 | 9.28 | 8.28 | 7.28 | ||||||
| 11.29 | 10.29 | 9.29 | 8.29 | |||||||
| 11.30 | 10.30 | 9.30 | ||||||||
| 11.31 | 10.31 | |||||||||
| 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
With the marking of the different types of rows complete we now have a visual overview of the king list. Sure, it does not look like much, but have patience. When we reorganise the king list into 21 columns as per a half-size Vorlage E, a symmetrical pattern emerges:
| 7.1 | Kingship formula | 7.1 | Lost kingship formula | 7.1 | Partial kingship formula |
| 7.1 | Heading | 7.1 | Lost Heading | 7.1 | Summation |
| 7.1 | Ditto mark | 7.1 | Partial formula for founder of dynasty | ||
| Row ↓ | C O L U M N | Row ↓ | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | ||
| 1 | 11.27 | 11.8 | 10.22 | 10.6 | 9.20 | 9.4 | 8.18 | 8.3 | 7.16 | 7.1 | 6.11 | 5.22 | 5.7 | 4.19 | 4.5 | 3.16 | 3.2 | 2.15 | 2.2 | 1.14 | 1.1 | 1 |
| 2 | 11.28 | 11.9 | 10.23 | 10.7 | 9.21 | 9.5 | 8.19 | 8.4 | 7.17 | 7.2 | 6.12 | 5.23 | 5.8 | 4.20 | 4.6 | 3.17 | 3.3 | 2.16 | 2.3 | 1.15 | 1.2 | 2 |
| 3 | 11.29 | 11.10 | 10.24 | 10.8 | 9.22 | 9.6 | 8.20 | 8.5 | 7.18 | 7.3 | 6.13 | 5.24 | 5.9 | 4.21 | 4.7 | 3.18 | 3.4 | 2.17 | 2.4 | 1.16 | 1.3 | 3 |
| 4 | 11.30 | 11.11 | 10.25 | 10.9 | 9.23 | 9.7 | 8.21 | 8.6 | 7.19 | 7.4 | 6.14 | 5.25 | 5.10 | 4.22 | 4.8 | 3.19 | 3.5 | 2.18 | 2.6 | 1.17 | 1.4 | 4 |
| 5 | 11.31 | 11.12 | 10.26 | 10.10 | 9.24 | 9.8 | 8.22 | 8.7 | 7.20 | 7.5 | 6.15 | 5.26 | 5.11 | 4.23 | 4.9 | 3.20 | 3.6 | 2.19 | 2.7 | 1.18 | 1.5 | 5 |
| 6 | 12.1 | 11.13 | 10.27 | 10.11 | 9.25 | 9.9 | 8.23 | 8.8 | 7.21 | 7.6 | 6.16 | 6.1 | 5.12 | 4.24 | 4.10 | 3.21 | 3.7 | 2.20 | 2.7 | 1.19 | 1.6 | 6 |
| 7 | 12.2 | 11.14 | 10.28 | 10.12 | 9.26 | 9.10 | 8.24 | 8.9 | 7.22 | 7.7 | 6.17 | 6.2 | 5.13 | 4.25 | 4.11 | 3.22 | 3.8 | 2.21 | 2.8 | 1.20 | 1.7 | 7 |
| 8 | 12.3 | 11.15 | 10.29 | 10.13 | 9.27 | 9.11 | 8.25 | 8.10 | 7.23 | 7.8 | 6.18 | 6.3 | 5.14 | 4.26 | 4.12 | 3.23 | 3.9 | 2.22 | 2.9 | 1.21 | 1.8 | 8 |
| 9 | 12.4 | 11.16 | 10.30 | 10.14 | 9.28 | 9.12 | 8.26 | 8.11 | 7.24 | 7.9 | 6.19 | 6.4 | 5.15 | 5.1 | 4.13 | 3.24 | 3.10 | 2.23 | 2.10 | 1.22 | 1.9 | 9 |
| 10 | 12.5 | 11.17 | 10.31 | 10.15 | 9.29 | 9.13 | 8.27 | 8.12 | 7.25 | 7.10 | 6.20 | 6.5 | 5.16 | 5.2 | 4.14 | 3.25 | 3.11 | 2.24 | 2.11 | 1.23 | 1.10 | 10 |
| 11 | 12.6 | 11.18 | 11.1 | 10.16 | 9.30 | 9.14 | 8.28 | 8.13 | 7.26 | 7.11 | 6.21 | 6.6 | 5.17 | 5.3 | 4.15 | 4.1 | 3.12 | 2.25 | 2.12 | 1.24 | 1.11 | 11 |
| 12 | 12.7 | 11.19 | 11.2 | 10.17 | 10.1 | 9.15 | 8.29 | 8.14 | 7.27 | 7.12 | 6.22 | 6.7 | 5.18 | 5.4 | 4.16 | 4.2 | 3.13 | 2.26 | 2.13 | 1.25 | 1.12 | 12 |
| 13 | 12.8 | 11.20 | 11.3 | 10.18 | 10.2 | 9.16 | 9.1 | 8.15 | 7.28 | 7.13 | 6.23 | 6.8 | 5.19 | 5.5 | 4.17 | 4.3 | 3.15 | 3.1 | 2.14 | 2.1 | 1.13 | 13 |
| 14 | 12.9 | 11.21 | 11.4 | 10.19 | 10.3 | 9.17 | 9.2 | 8.16 | 8.1 | 7.14 | 6.24 | 6.9 | 5.20 | 5.6 | 4.18 | 4.4 | 14 | |||||
| 15 | 12.10 | 11.22 | 11.5 | 10.20 | 10.4 | 9.18 | 9.3 | 8.17 | 8.2 | 7.15 | 6.25 | 6.10 | 5.21 | 15 | ||||||||
| 16 | 12.11 | 11.23 | 11.6 | 10.21 | 10.5 | 9.19 | 16 | |||||||||||||||
| 17 | 12.12 | 11.24 | 11.7 | 17 | ||||||||||||||||||
| 18 | 12.13 | 11.25 | 18 | |||||||||||||||||||
| 19 | 12.14 | 11.26 | 19 | |||||||||||||||||||
| Row | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | Row |
| C O L U M N | ||||||||||||||||||||||
It appears to be compelling proof, yet it is, as usual, only a theory. You might certainly argue that the evidence was manipulated to meet a presupposition. However, in the absence of a better theory...
Bibliography
- Helck, Wolfgang. “Untersuchungen zu Manetho und den ägyptischen Königslisten”. UGAA 18 (Berlin: 1956).
- Ryholt, Kim. The Political Situation in Egypt during the Second Intermediate Period. Copenhagen: 1997.